Goodness of Fit and Shepard Plot for Nonmetric Multidimensional Scaling

Function goodness.metaMDS find goodness of fit measure for points in nonmetric multidimensional scaling, and function stressplot makes a Shepard diagram.

Usage

# S3 method for metaMDS
goodness(object, dis, ...)
# S3 method for default
stressplot(object, dis, pch, p.col = "blue", l.col = "red", 
    lwd = 2, ...)

Arguments

object: A result object from metaMDS, monoMDS or isoMDS.
dis: Dissimilarities. This should not be used with metaMDS or monoMDS, but must be used with isoMDS.
pch: Plotting character for points. Default is dependent on the number of points.
p.col, l.col: Point and line colours.
lwd: Line width. For monoMDS the default is lwd = 1 if more than two lines are drawn, and lwd = 2 otherwise.
...: Other parameters to functions, e.g. graphical parameters.

Details

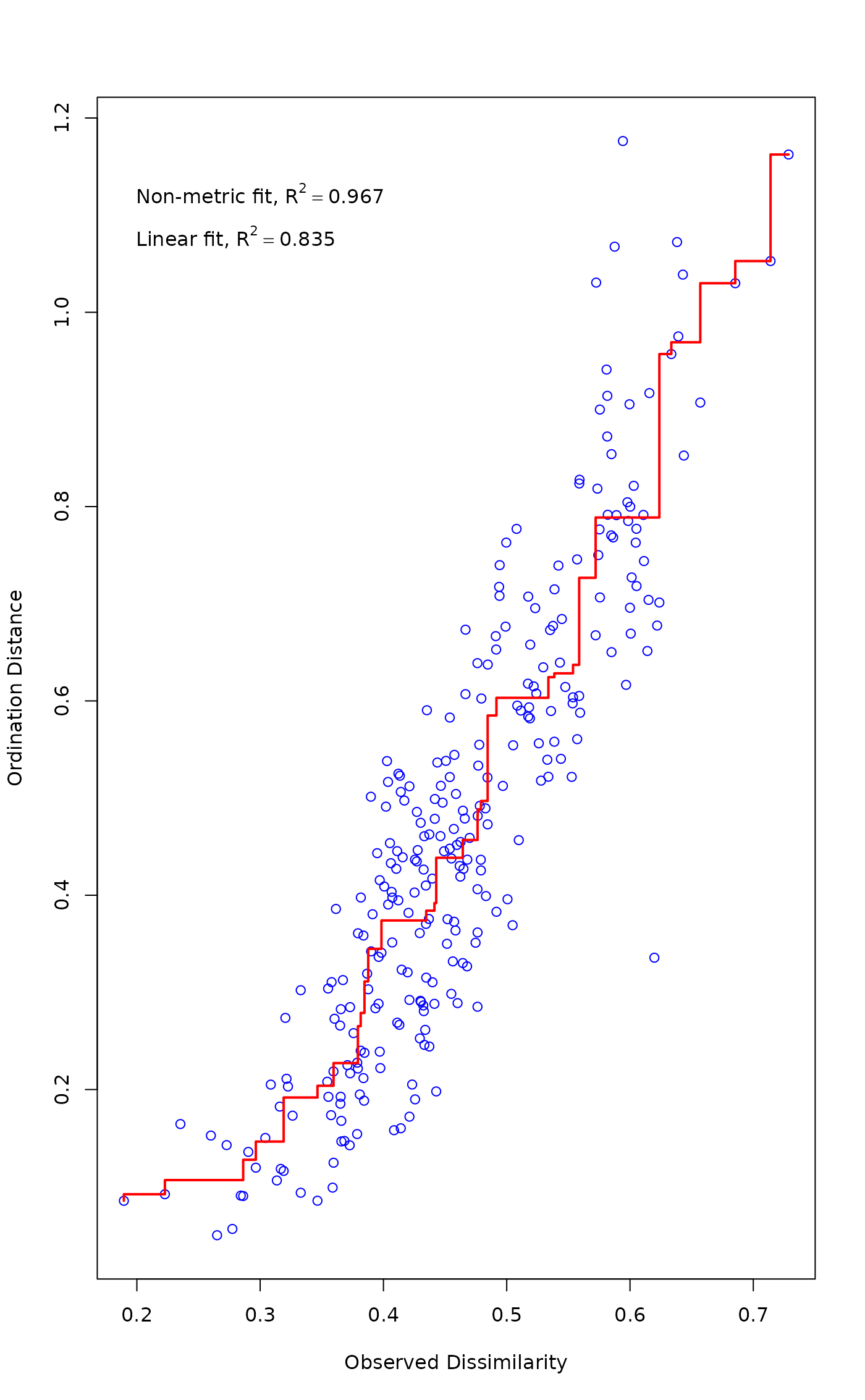
Function goodness.metaMDS finds a goodness of fit statistic for observations (points). This is defined so that sum of squared values is equal to squared stress. Large values indicate poor fit. The absolute values of the goodness statistic depend on the definition of the stress: isoMDS expresses stress in percents, and therefore its goodness values are 100 times higher than those of monoMDS which expresses the stress as a proportion.

Function stressplot draws a Shepard diagram which is a plot of ordination distances and monotone or linear fit line against original dissimilarities. In addition, it displays two correlation-like statistics on the goodness of fit in the graph. The nonmetric fit is based on stress \(S\) and defined as \(R^2 = 1-S^2\). The “linear fit” is the squared correlation between fitted values and ordination distances. For monoMDS, the “linear fit” and \(R^2\) from “stress type 2” are equal.

Both functions can be used with metaMDS, monoMDS and isoMDS. The original dissimilarities should not be given for monoMDS or metaMDS results (the latter tries to reconstruct the dissimilarities using metaMDSredist if isoMDS was used as its engine). With isoMDS the dissimilarities must be given. In either case, the functions inspect that dissimilarities are consistent with current ordination, and refuse to analyse inconsistent dissimilarities. Function goodness.metaMDS is generic in vegan, but you must spell its name completely with isoMDS which has no class.

Value

Function goodness returns a vector of values. Function

stressplot returns invisibly an object with items for original dissimilarities, ordination distances and fitted values.

Author

Jari Oksanen.

Examples

data(varespec)
mod <- metaMDS(varespec)
#> Square root transformation
#> Wisconsin double standardization
#> Run 0 stress 0.1843196 
#> Run 1 stress 0.1969805 
#> Run 2 stress 0.1974407 
#> Run 3 stress 0.3045657 
#> Run 4 stress 0.1955836 
#> Run 5 stress 0.2281606 
#> Run 6 stress 0.2109611 
#> Run 7 stress 0.195049 
#> Run 8 stress 0.2102718 
#> Run 9 stress 0.1825658 
#> ... New best solution
#> ... Procrustes: rmse 0.04163315  max resid 0.1518391 
#> Run 10 stress 0.1967393 
#> Run 11 stress 0.1825658 
#> ... New best solution
#> ... Procrustes: rmse 6.49348e-06  max resid 1.721092e-05 
#> ... Similar to previous best
#> Run 12 stress 0.241719 
#> Run 13 stress 0.2100656 
#> Run 14 stress 0.1985581 
#> Run 15 stress 0.2005512 
#> Run 16 stress 0.224054 
#> Run 17 stress 0.2101148 
#> Run 18 stress 0.2127526 
#> Run 19 stress 0.3043888 
#> Run 20 stress 0.2706197 
#> *** Best solution repeated 1 times
stressplot(mod)

gof <- goodness(mod)
gof
#>  [1] 0.02984513 0.03513722 0.04189121 0.04598275 0.04003128 0.03441456
#>  [7] 0.03294852 0.03050129 0.03060721 0.02994054 0.03526380 0.02621411
#> [13] 0.03831022 0.02980913 0.03369665 0.02225887 0.03561536 0.03505284
#> [19] 0.06577479 0.03268381 0.03503155 0.02956635 0.05167962 0.04601989
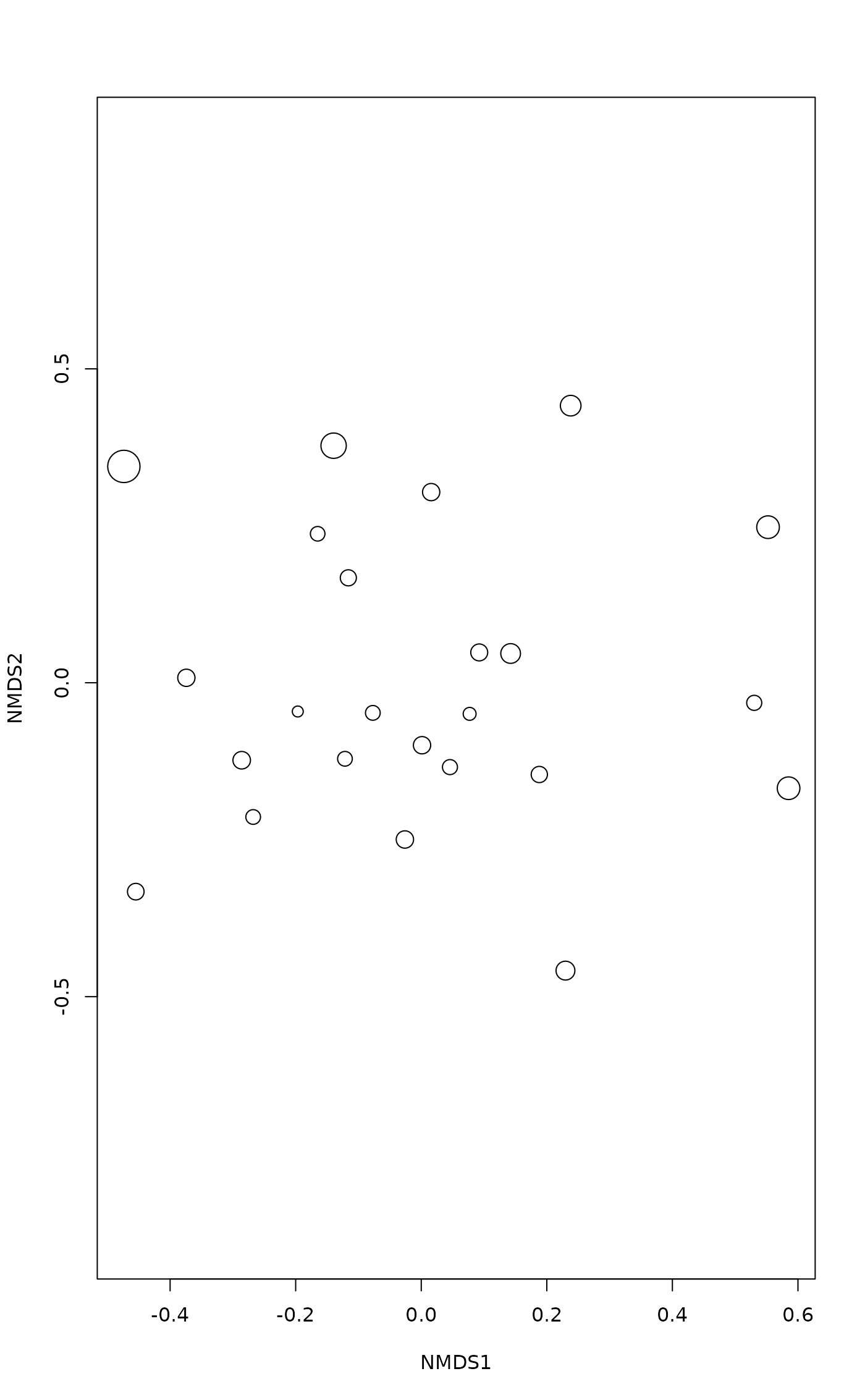
plot(mod, display = "sites", type = "n")
points(mod, display = "sites", cex = 2*gof/mean(gof))