Indices of beta Diversity

The function estimates any of the 24 indices of beta diversity reviewed by Koleff et al. (2003). Alternatively, it finds the co-occurrence frequencies for triangular plots (Koleff et al. 2003).

Usage

betadiver(x, method = NA, order = FALSE, help = FALSE, ...)
# S3 method for class 'betadiver'
plot(x, ...)
# S3 method for class 'betadiver'
scores(x, triangular = TRUE, ...)

Arguments

x: Community data matrix, or the betadiver result for plot and scores functions.
method: The index of beta diversity as defined in Koleff et al. (2003), Table 1. You can use either the subscript of \(\beta\) or the number of the index. See argument help below.
order: Order sites by increasing number of species. This will influence the configuration in the triangular plot and non-symmetric indices.
help: Show the numbers, subscript names and the defining equations of the indices and exit.
triangular: Return scores suitable for triangular plotting of proportions. If FALSE, returns a 3-column matrix of raw counts.
...: Other arguments to functions.

Details

The most commonly used index of beta diversity is \(\beta_w = S/\alpha - 1\), where \(S\) is the total number of species, and \(\alpha\) is the average number of species per site (Whittaker 1960). A drawback of this model is that \(S\) increases with sample size, but the expectation of \(\alpha\) remains constant, and so the beta diversity increases with sample size. A solution to this problem is to study the beta diversity of pairs of sites (Marion et al. 2017). If we denote the number of species shared between two sites as \(a\) and the numbers of unique species (not shared) as \(b\) and \(c\), then \(S = a + b + c\) and \(\alpha = (2 a + b + c)/2\) so that \(\beta_w = (b+c)/(2 a + b + c)\). This is the Sørensen dissimilarity as defined in vegan function vegdist with argument binary = TRUE. Many other indices are dissimilarity indices as well.

Function betadiver finds all indices reviewed by Koleff et al. (2003). All these indices could be found with function designdist, but the current function provides a conventional shortcut. The function only finds the indices. The proper analysis must be done with functions such as betadisper, adonis2 or mantel.

The indices are directly taken from Table 1 of Koleff et al. (2003), and they can be selected either by the index number or the subscript name used by Koleff et al. The numbers, names and defining equations can be seen using betadiver(help = TRUE). In all cases where there are two alternative forms, the one with the term \(-1\) is used. There are several duplicate indices, and the number of distinct alternatives is much lower than 24 formally provided. The formulations used in functions differ occasionally from those in Koleff et al. (2003), but they are still mathematically equivalent. With method = NA, no index is calculated, but instead an object of class betadiver is returned. 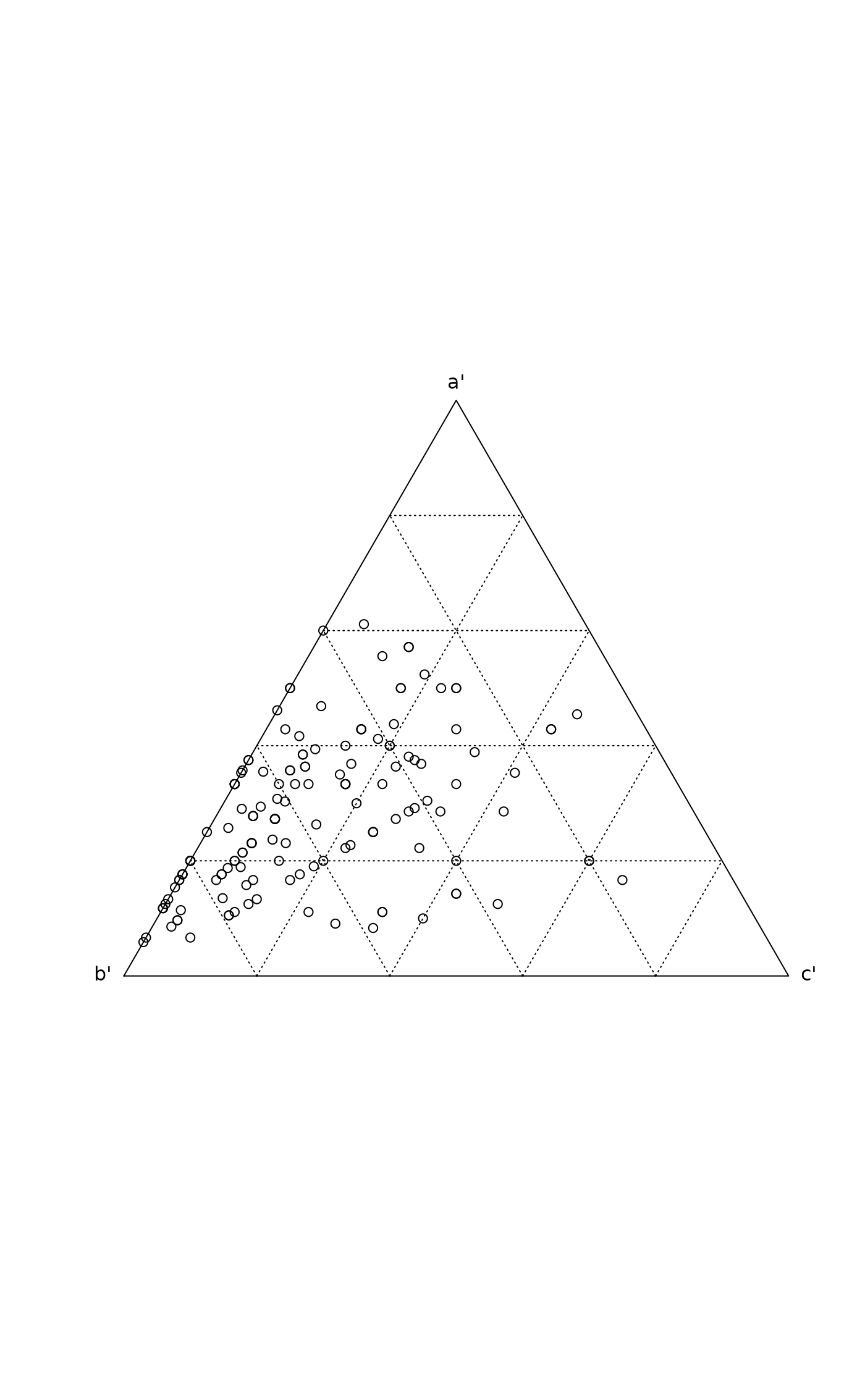This is a list of elements a, b and c. Function plot can be used to display the proportions of these elements in triangular plot as suggested by Koleff et al. (2003), and scores extracts the triangular coordinates or the raw scores. Function plot returns invisibly the triangular coordinates as an "ordiplot" object.

Value

With method = NA, the function returns an object of class "betadisper" with elements a, b, and c. If method is specified, the function returns a "dist" object which can be used in any function analysing dissimilarities. For beta diversity, particularly useful functions are betadisper to study the betadiversity in groups, adonis2 for any model, and mantel to compare beta diversities to other dissimilarities or distances (including geographical distances). Although betadiver returns a "dist" object, some indices are similarities and cannot be used as such in place of dissimilarities, but that is a user error. Functions 10 ("j"), 11 ("sor") and 21 ("rlb") are similarity indices. Function sets argument "maxdist" similarly as vegdist, using NA when there is no fixed upper limit, and 0 for similarities.

References

Baselga, A. (2010) Partitioning the turnover and nestedness components of beta diversity. Global Ecology and Biogeography 19, 134–143.

Koleff, P., Gaston, K.J. and Lennon, J.J. (2003) Measuring beta diversity for presence-absence data. Journal of Animal Ecology 72, 367–382.

Marion, Z.H., Fordyce, J.A. and Fitzpatrick, B.M. (2017) Pairwise beta diversity resolves an underappreciated source of confusion in calculating species turnover. Ecology 98, 933–939.

Whittaker, R.H. (1960) Vegetation of Siskiyou mountains, Oregon and California. Ecological Monographs 30, 279–338.

Author

Jari Oksanen

Warning

Some indices return similarities instead of dissimilarities.

Examples

## Raw data and plotting
data(sipoo)
m <- betadiver(sipoo)
plot(m)

## The indices
betadiver(help=TRUE)
#> 1 "w" = (b+c)/(2*a+b+c)
#> 2 "-1" = (b+c)/(2*a+b+c)
#> 3 "c" = (b+c)/2
#> 4 "wb" = b+c
#> 5 "r" = 2*b*c/((a+b+c)^2-2*b*c)
#> 6 "I" = log(2*a+b+c) - 2*a*log(2)/(2*a+b+c) - ((a+b)*log(a+b) +
#> (a+c)*log(a+c)) / (2*a+b+c)
#> 7 "e" = exp(log(2*a+b+c) - 2*a*log(2)/(2*a+b+c) - ((a+b)*log(a+b) +
#> (a+c)*log(a+c)) / (2*a+b+c))-1
#> 8 "t" = (b+c)/(2*a+b+c)
#> 9 "me" = (b+c)/(2*a+b+c)
#> 10 "j" = a/(a+b+c)
#> 11 "sor" = 2*a/(2*a+b+c)
#> 12 "m" = (2*a+b+c)*(b+c)/(a+b+c)
#> 13 "-2" = pmin.int(b,c)/(pmax.int(b,c)+a)
#> 14 "co" = (a*c+a*b+2*b*c)/(2*(a+b)*(a+c))
#> 15 "cc" = (b+c)/(a+b+c)
#> 16 "g" = (b+c)/(a+b+c)
#> 17 "-3" = pmin.int(b,c)/(a+b+c)
#> 18 "l" = (b+c)/2
#> 19 "19" = 2*(b*c+1)/(a+b+c)/(a+b+c-1)
#> 20 "hk" = (b+c)/(2*a+b+c)
#> 21 "rlb" = a/(a+c)
#> 22 "sim" = pmin.int(b,c)/(pmin.int(b,c)+a)
#> 23 "gl" = 2*abs(b-c)/(2*a+b+c)
#> 24 "z" = (log(2)-log(2*a+b+c)+log(a+b+c))/log(2)
## The basic Whittaker index
d <- betadiver(sipoo, "w")
## This should be equal to Sorensen index (binary Bray-Curtis in
## vegan)
range(d - vegdist(sipoo, binary=TRUE))
#> [1] 0 0