Multivariate homogeneity of groups dispersions (variances)

Implements Marti Anderson's PERMDISP2 procedure for the analysis of multivariate homogeneity of group dispersions (variances). betadisper is a multivariate analogue of Levene's test for homogeneity of variances. Non-euclidean distances between objects and group centres (centroids or medians) are handled by reducing the original distances to principal coordinates. This procedure has latterly been used as a means of assessing beta diversity. There are anova, scores, plot and boxplot methods.

TukeyHSD.betadisper creates a set of confidence intervals on the differences between the mean distance-to-centroid of the levels of the grouping factor with the specified family-wise probability of coverage. The intervals are based on the Studentized range statistic, Tukey's 'Honest Significant Difference' method.

Usage

betadisper(d, group, type = c("median","centroid"), bias.adjust = FALSE,
       sqrt.dist = FALSE, add = FALSE)

# S3 method for class 'betadisper'
anova(object, ...)

# S3 method for class 'betadisper'
scores(x, display = c("sites", "centroids"),
       choices = c(1,2), ...)

# S3 method for class 'betadisper'
eigenvals(x, ...)

# S3 method for class 'betadisper'
plot(x, axes = c(1,2), cex = 0.7,
     pch = seq_len(ng), col = NULL, lty = "solid", lwd = 1, hull = TRUE,
     ellipse = FALSE, conf,
     segments = TRUE, seg.col = "grey", seg.lty = lty, seg.lwd = lwd,
     label = TRUE, label.cex = 1,
     ylab, xlab, main, sub, ...)

# S3 method for class 'betadisper'
boxplot(x, ylab = "Distance to centroid", ...)

# S3 method for class 'betadisper'
TukeyHSD(x, which = "group", ordered = FALSE,
         conf.level = 0.95, ...)

# S3 method for class 'betadisper'
print(x, digits = max(3, getOption("digits") - 3),
                           neigen = 8, ...)

betadistances(x, ...)

Arguments

d

a distance structure such as that returned by dist, betadiver or vegdist.

group

vector describing the group structure, usually a factor or an object that can be coerced to a factor using as.factor. Can consist of a factor with a single level (i.e., one group).

type

the type of analysis to perform. Use the spatial median or the group centroid? The spatial median is now the default.

bias.adjust

logical: adjust for small sample bias in beta diversity estimates?

sqrt.dist

Take square root of dissimilarities. This often euclidifies dissimilarities.

add

Add a constant to the non-diagonal dissimilarities such that all eigenvalues are non-negative in the underlying Principal Co-ordinates Analysis (see wcmdscale for details). Choice "lingoes" (or TRUE) use the recommended method of Legendre & Anderson (1999: “method 1”) and "cailliez" uses their “method 2”.

display

character; partial match to access scores for "sites" or "species".

object, x

an object of class "betadisper", the result of a call to betadisper.

choices, axes

the principal coordinate axes wanted.

hull

logical; should the convex hull for each group be plotted?

ellipse

logical; should the standard deviation data ellipse for each group be plotted?

conf

Expected fractions of data coverage for data ellipses, e.g. 0.95. The default is to draw a 1 standard deviation data ellipse, but if supplied, conf is multiplied with the corresponding value found from the Chi-squared distribution with 2df to provide the requested coverage (probability contour).

pch

plot symbols for the groups, a vector of length equal to the number of groups.

col

colors for the plot symbols and centroid labels for the groups, a vector of length equal to the number of groups.

lty, lwd

linetype, linewidth for convex hulls and confidence ellipses.

segments

logical; should segments joining points to their centroid be drawn?

seg.col

colour to draw segments between points and their centroid. Can be a vector, in which case one colour per group.

seg.lty, seg.lwd

linetype and line width for segments.

label

logical; should the centroids by labelled with their respective factor label?

label.cex

numeric; character expansion for centroid labels.

cex, ylab, xlab, main, sub

graphical parameters. For details, see plot.default.

which

A character vector listing terms in the fitted model for which the intervals should be calculated. Defaults to the grouping factor.

ordered

logical; see TukeyHSD.

conf.level

A numeric value between zero and one giving the family-wise confidence level to use.

digits, neigen

numeric; for the print method, sets the number of digits to use (as per print.default) and the maximum number of axes to display eigenvalues for, repsectively.

...

arguments, including graphical parameters (for plot.betadisper and boxplot.betadisper), passed to other methods.

Details

One measure of multivariate dispersion (variance) for a group of samples is to calculate the average distance of group members to the group centroid or spatial median (both referred to as 'centroid' from now on unless stated otherwise) in multivariate space. To test if the dispersions (variances) of one or more groups are different, the distances of group members to the group centroid are subject to ANOVA. This is a multivariate analogue of Levene's test for homogeneity of variances if the distances between group members and group centroids is the Euclidean distance.

However, better measures of distance than the Euclidean distance are available for ecological data. These can be accommodated by reducing the distances produced using any dissimilarity coefficient to principal coordinates, which embeds them within a Euclidean space. The analysis then proceeds by calculating the Euclidean distances between group members and the group centroid on the basis of the principal coordinate axes rather than the original distances.

Non-metric dissimilarity coefficients can produce principal coordinate axes that have negative Eigenvalues. These correspond to the imaginary, non-metric part of the distance between objects. If negative Eigenvalues are produced, we must correct for these imaginary distances.

The distance to its centroid of a point is $$z_{ij}^c = \sqrt{\Delta^2(u_{ij}^+, c_i^+) - \Delta^2(u_{ij}^-, c_i^-)},$$ where \(\Delta^2\) is the squared Euclidean distance between \(u_{ij}\), the principal coordinate for the \(j\)th point in the \(i\)th group, and \(c_i\), the coordinate of the centroid for the \(i\)th group. The super-scripted ‘\(+\)’ and ‘\(-\)’ indicate the real and imaginary parts respectively. This is equation (3) in Anderson (2006). If the imaginary part is greater in magnitude than the real part, then we would be taking the square root of a negative value, resulting in NaN, and these cases are changed to zero distances (with a warning). This is in line with the behaviour of Marti Anderson's PERMDISP2 programme. Function betadistances returns distances from all points to all centroids. Moreover, it gives the original group and nearest group for each point.

To test if one or more groups is more variable than the others, ANOVA of the distances to group centroids can be performed and parametric theory used to interpret the significance of \(F\). An alternative is to use a permutation test. permutest.betadisper permutes model residuals to generate a permutation distribution of \(F\) under the Null hypothesis of no difference in dispersion between groups.

Pairwise comparisons of group mean dispersions can also be performed using permutest.betadisper. An alternative to the classical comparison of group dispersions, is to calculate Tukey's Honest Significant Differences between groups, via TukeyHSD.betadisper. This is a simple wrapper to TukeyHSD. The user is directed to read the help file for TukeyHSD before using this function. In particular, note the statement about using the function with unbalanced designs.

The results of the analysis can be visualised using the plot and boxplot methods. The distances of points to all centroids (group) can be found with function betadistances.

One additional use of these functions is in assessing beta diversity (Anderson et al 2006). Function betadiver provides some popular dissimilarity measures for this purpose.

As noted in passing by Anderson (2006) and in a related context by O'Neill (2000), estimates of dispersion around a central location (median or centroid) that is calculated from the same data will be biased downward. This bias matters most when comparing diversity among treatments with small, unequal numbers of samples. Setting bias.adjust=TRUE when using betadisper imposes a \(\sqrt{n/(n-1)}\) correction (Stier et al. 2013).

Value

The anova method returns an object of class "anova" inheriting from class "data.frame".

The scores method returns a list with one or both of the components "sites" and "centroids".

The plot function invisibly returns an object of class "ordiplot", a plotting structure which can be used by identify.ordiplot (to identify the points) or other functions in the ordiplot family.

The boxplot function invisibly returns a list whose components are documented in boxplot.

eigenvals.betadisper returns a named vector of eigenvalues.

TukeyHSD.betadisper returns a list. See TukeyHSD for further details.

betadisper returns a list of class "betadisper" with the following components:

eig

numeric; the eigenvalues of the principal coordinates analysis.

vectors

matrix; the eigenvectors of the principal coordinates analysis.

distances

numeric; the Euclidean distances in principal coordinate space between the samples and their respective group centroid or median.

group

factor; vector describing the group structure

centroids

matrix; the locations of the group centroids or medians on the principal coordinates.

group.distances

numeric; the mean distance to each group centroid or median.

call

the matched function call.

Note

If group consists of a single level or group, then the anova and permutest methods are not appropriate and if used on such data will stop with an error.

Missing values in either d or group will be removed prior to performing the analysis.

Warning

Stewart Schultz noticed that the permutation test for type="centroid" had the wrong type I error and was anti-conservative. As such, the default for type has been changed to "median", which uses the spatial median as the group centroid. Tests suggests that the permutation test for this type of analysis gives the correct error rates.

References

Anderson, M.J. (2006) Distance-based tests for homogeneity of multivariate dispersions. Biometrics 62, 245–253.

Anderson, M.J., Ellingsen, K.E. & McArdle, B.H. (2006) Multivariate dispersion as a measure of beta diversity. Ecology Letters 9, 683–693.

O'Neill, M.E. (2000) A Weighted Least Squares Approach to Levene's Test of Homogeneity of Variance. Australian & New Zealand Journal of Statistics 42, 81-–100.

Stier, A.C., Geange, S.W., Hanson, K.M., & Bolker, B.M. (2013) Predator density and timing of arrival affect reef fish community assembly. Ecology 94, 1057–1068.

Author

Gavin L. Simpson; bias correction by Adrian Stier and Ben Bolker.

See also

permutest.betadisper, anova.lm, scores, boxplot, TukeyHSD. Further measure of beta diversity can be found in betadiver.

Examples

data(varespec)

## Bray-Curtis distances between samples
dis <- vegdist(varespec)

## First 16 sites grazed, remaining 8 sites ungrazed
groups <- factor(c(rep(1,16), rep(2,8)), labels = c("grazed","ungrazed"))

## Calculate multivariate dispersions
mod <- betadisper(dis, groups)
mod
#> 
#> 	Homogeneity of multivariate dispersions
#> 
#> Call: betadisper(d = dis, group = groups)
#> 
#> No. of Positive Eigenvalues: 15
#> No. of Negative Eigenvalues: 8
#> 
#> Average distance to median:
#>   grazed ungrazed 
#>   0.3926   0.2706 
#> 
#> Eigenvalues for PCoA axes:
#> (Showing 8 of 23 eigenvalues)
#>  PCoA1  PCoA2  PCoA3  PCoA4  PCoA5  PCoA6  PCoA7  PCoA8 
#> 1.7552 1.1334 0.4429 0.3698 0.2454 0.1961 0.1751 0.1284 

## Perform test
anova(mod)
#> Analysis of Variance Table
#> 
#> Response: Distances
#>           Df  Sum Sq  Mean Sq F value  Pr(>F)  
#> Groups     1 0.07931 0.079306  4.6156 0.04295 *
#> Residuals 22 0.37801 0.017182                  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

## Permutation test for F
permutest(mod, pairwise = TRUE, permutations = 99)
#> 
#> Permutation test for homogeneity of multivariate dispersions
#> Permutation: free
#> Number of permutations: 99
#> 
#> Response: Distances
#>           Df  Sum Sq  Mean Sq      F N.Perm Pr(>F)  
#> Groups     1 0.07931 0.079306 4.6156     99   0.09 .
#> Residuals 22 0.37801 0.017182                       
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Pairwise comparisons:
#> (Observed p-value below diagonal, permuted p-value above diagonal)
#>           grazed ungrazed
#> grazed               0.09
#> ungrazed 0.04295         

## Tukey's Honest Significant Differences
(mod.HSD <- TukeyHSD(mod))
#>   Tukey multiple comparisons of means
#>     95% family-wise confidence level
#> 
#> Fit: aov(formula = distances ~ group, data = df)
#> 
#> $group
#>                       diff        lwr          upr     p adj
#> ungrazed-grazed -0.1219422 -0.2396552 -0.004229243 0.0429502
#> 
plot(mod.HSD)


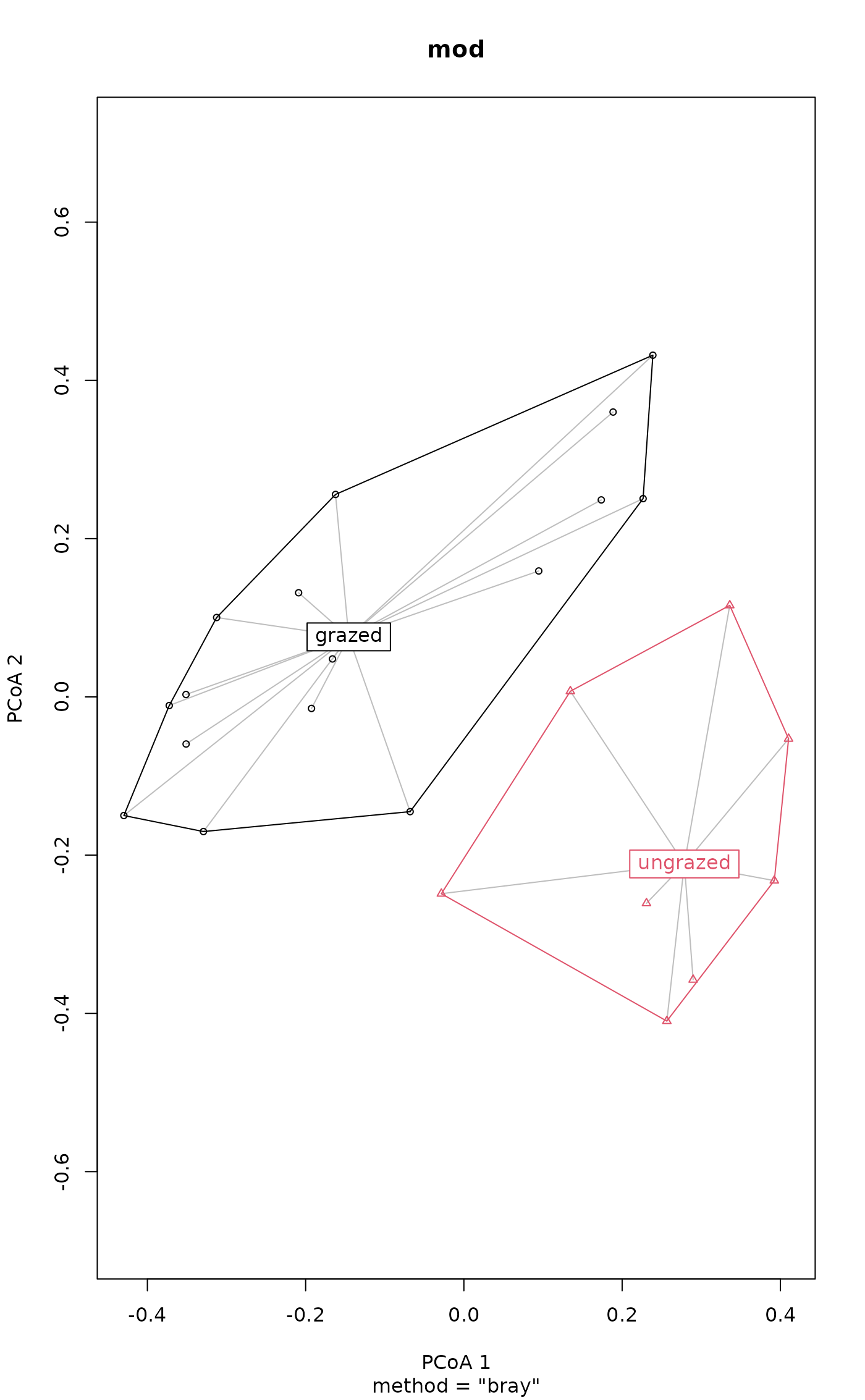
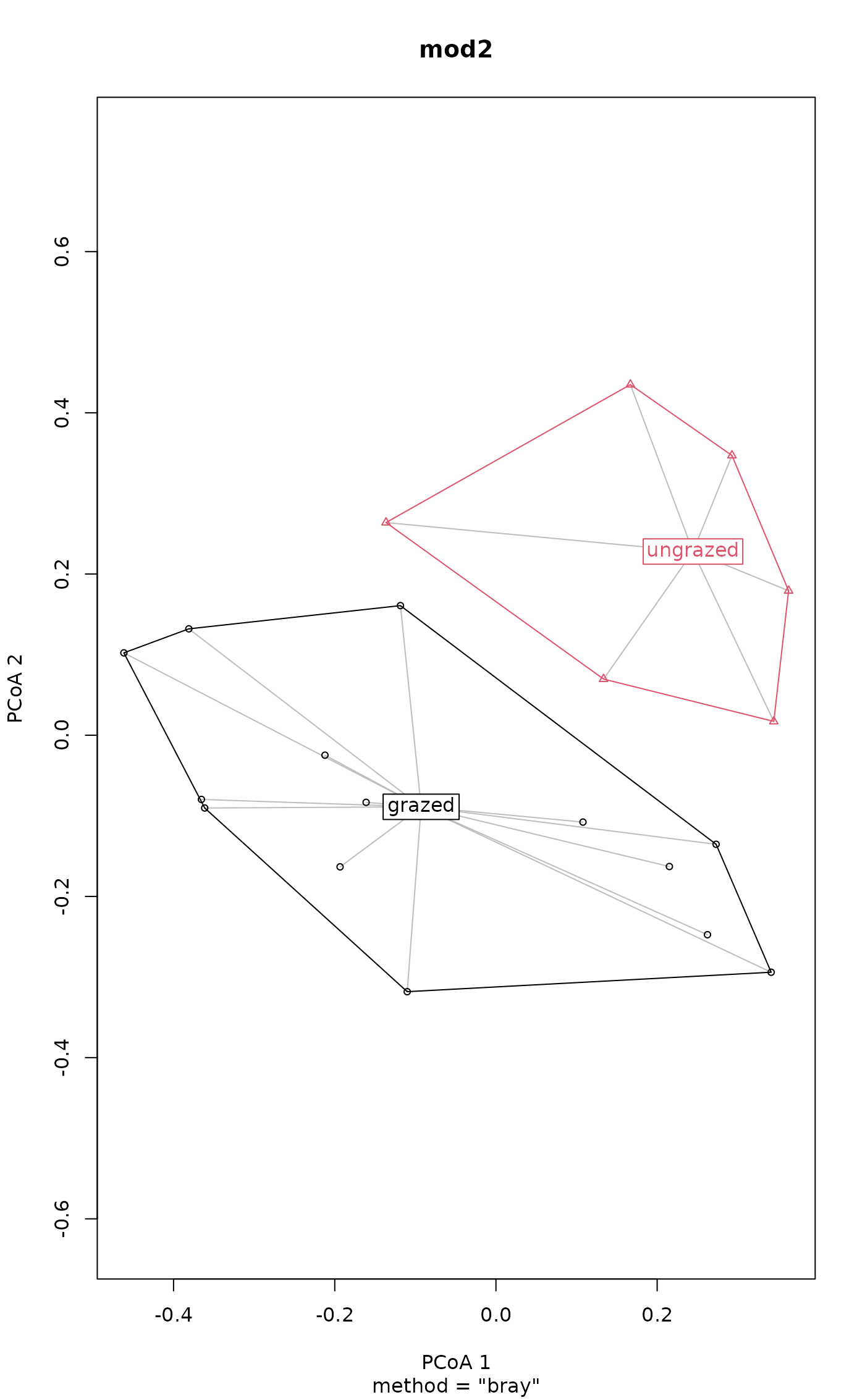
## Plot  and show the groups and distances to centroids on the
## first two PCoA axes
plot(mod)

betadistances(mod)
#>       group  nearest    grazed  ungrazed
#> 18   grazed   grazed 0.3314940 0.4876932
#> 15   grazed   grazed 0.2448593 0.6867177
#> 24   grazed   grazed 0.4087618 0.7202852
#> 27   grazed   grazed 0.4055027 0.6716925
#> 23   grazed   grazed 0.2711717 0.5859224
#> 19   grazed   grazed 0.3235683 0.4226658
#> 22   grazed   grazed 0.3540192 0.7143106
#> 16   grazed   grazed 0.3052699 0.6567417
#> 28   grazed   grazed 0.5804799 0.8350802
#> 13   grazed   grazed 0.4573620 0.5496107
#> 14   grazed   grazed 0.4346688 0.7480122
#> 20   grazed   grazed 0.2458315 0.5795502
#> 25   grazed   grazed 0.3544958 0.7270236
#> 7    grazed   grazed 0.5019108 0.6344208
#> 5    grazed   grazed 0.6029360 0.7048208
#> 6    grazed   grazed 0.4590746 0.5195341
#> 3  ungrazed ungrazed 0.5810524 0.2147308
#> 4  ungrazed ungrazed 0.5626172 0.4286653
#> 2  ungrazed ungrazed 0.6254225 0.1301314
#> 9  ungrazed ungrazed 0.6461171 0.2223194
#> 12 ungrazed ungrazed 0.5079965 0.0761938
#> 10 ungrazed ungrazed 0.6247805 0.1748861
#> 11 ungrazed ungrazed 0.3611882 0.3359708
#> 21 ungrazed   grazed 0.5694430 0.5822677

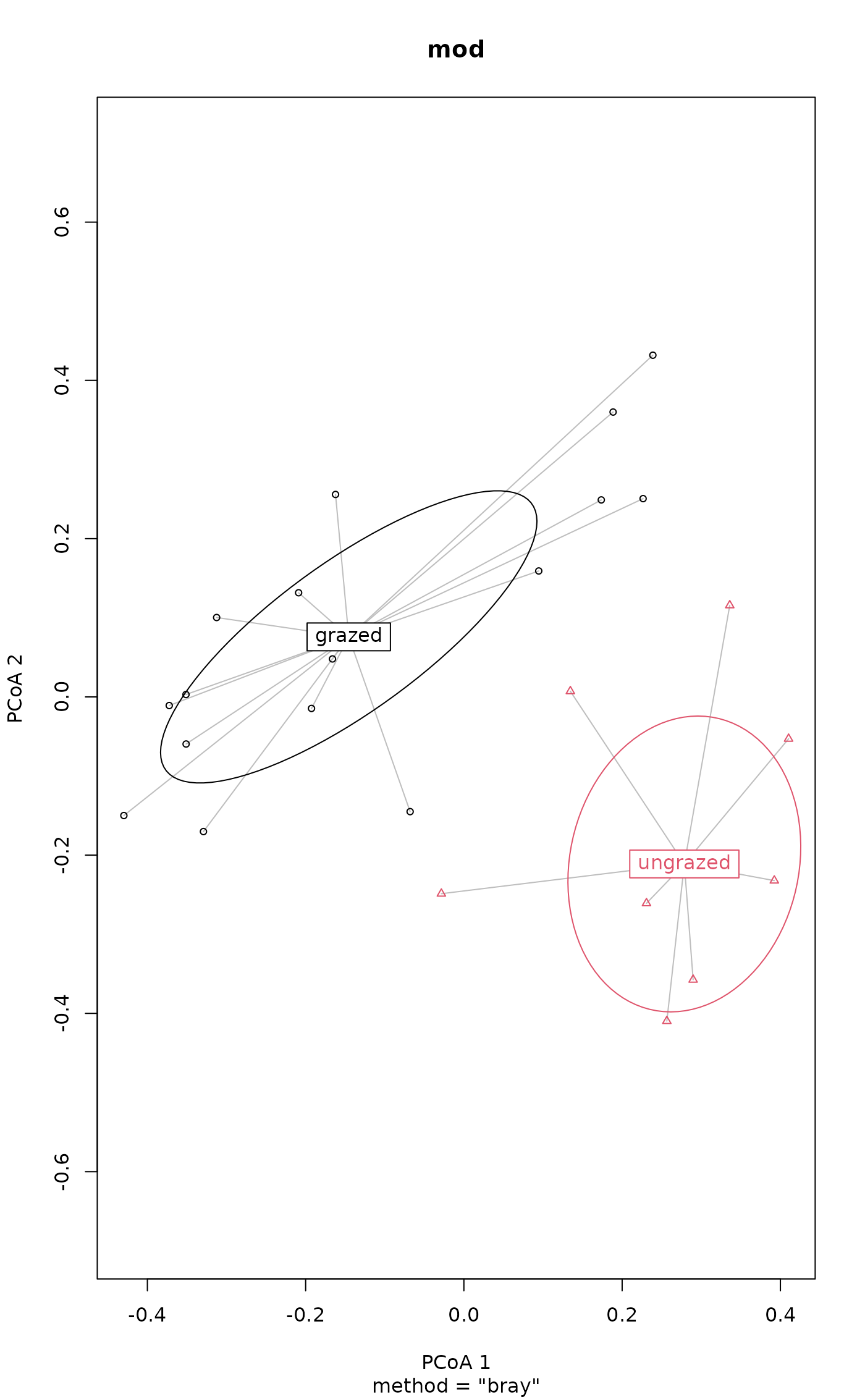
## with data ellipses instead of hulls
plot(mod, ellipse = TRUE, hull = FALSE) # 1 sd data ellipse

plot(mod, ellipse = TRUE, hull = FALSE, conf = 0.90) # 90% data ellipse


# plot with manual colour specification
my_cols <- c("#1b9e77", "#7570b3")
plot(mod, col = my_cols, pch = c(16,17), cex = 1.1)


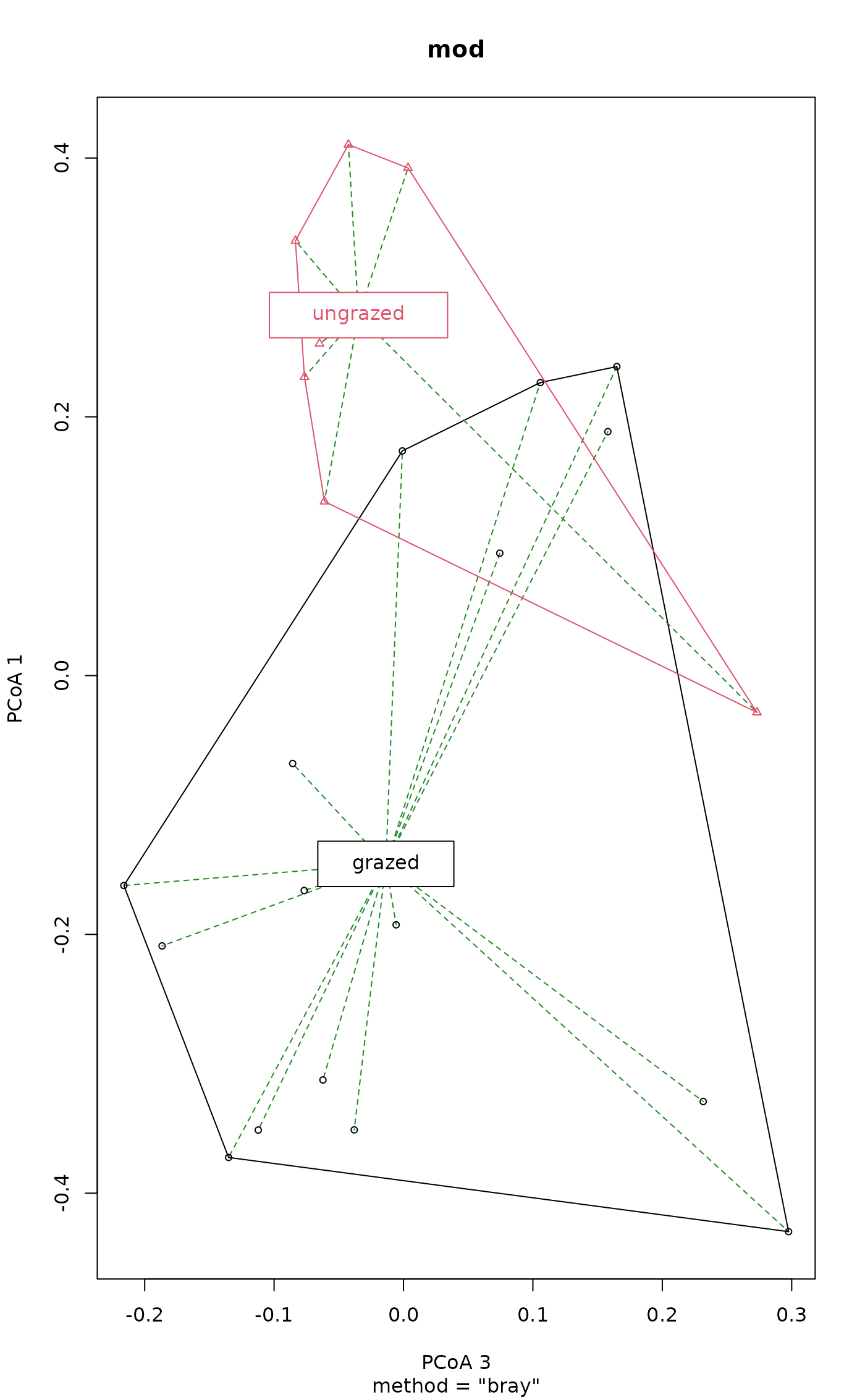
## can also specify which axes to plot, ordering respected
plot(mod, axes = c(3,1), seg.col = "forestgreen", seg.lty = "dashed")


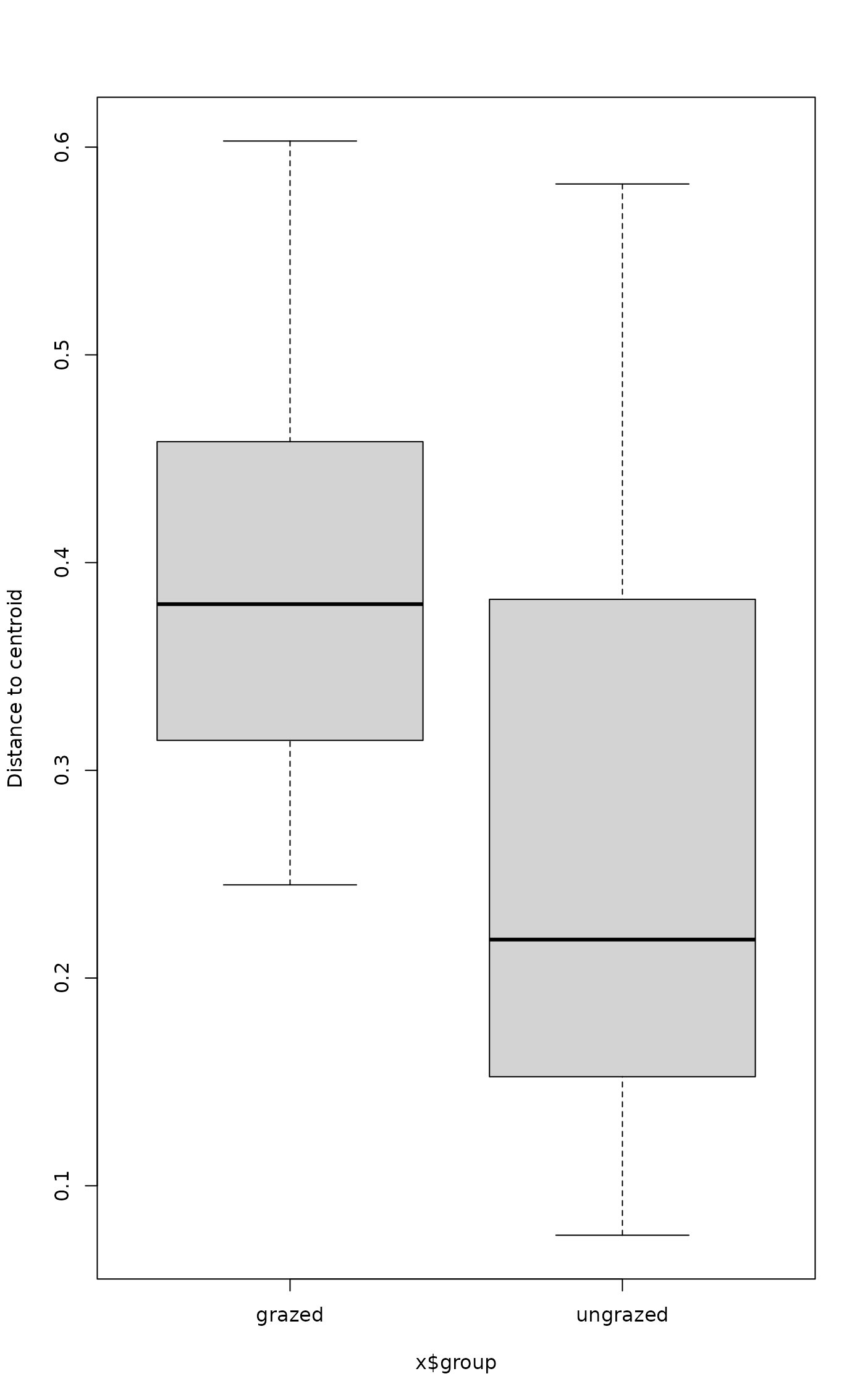
## Draw a boxplot of the distances to centroid for each group
boxplot(mod)


## `scores` and `eigenvals` also work
scrs <- scores(mod)
str(scrs)
#> List of 2
#>  $ sites    : num [1:24, 1:2] -0.0946 0.3125 0.3511 0.3291 0.1926 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : chr [1:24] "18" "15" "24" "27" ...
#>   .. ..$ : chr [1:2] "PCoA1" "PCoA2"
#>  $ centroids: num [1:2, 1:2] 0.1455 -0.2786 0.0758 -0.2111
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : chr [1:2] "grazed" "ungrazed"
#>   .. ..$ : chr [1:2] "PCoA1" "PCoA2"
head(scores(mod, 1:4, display = "sites"))
#>          PCoA1       PCoA2        PCoA3        PCoA4
#> 18 -0.09459373  0.15914576  0.074400844 -0.202466025
#> 15  0.31248809  0.10032751 -0.062243360  0.110844864
#> 24  0.35106507 -0.05954096 -0.038079447  0.095060928
#> 27  0.32914546 -0.17019348  0.231623720  0.019110623
#> 23  0.19259443 -0.01459250 -0.005679372 -0.209718312
#> 19  0.06794575 -0.14501690 -0.085645653  0.002431355
# group centroids/medians 
scores(mod, 1:4, display = "centroids")
#>               PCoA1       PCoA2       PCoA3      PCoA4
#> grazed    0.1455200  0.07584572 -0.01366220 -0.0178990
#> ungrazed -0.2786095 -0.21114993 -0.03475586  0.0220129
# eigenvalues from the underlying principal coordinates analysis
eigenvals(mod) 
#>      PCoA1      PCoA2      PCoA3      PCoA4      PCoA5      PCoA6      PCoA7 
#>  1.7552165  1.1334455  0.4429018  0.3698054  0.2453532  0.1960921  0.1751131 
#>      PCoA8      PCoA9     PCoA10     PCoA11     PCoA12     PCoA13     PCoA14 
#>  0.1284467  0.0971594  0.0759601  0.0637178  0.0583225  0.0394934  0.0172699 
#>     PCoA15     PCoA16     PCoA17     PCoA18     PCoA19     PCoA20     PCoA21 
#>  0.0051011 -0.0004131 -0.0064654 -0.0133147 -0.0253944 -0.0375105 -0.0480069 
#>     PCoA22     PCoA23 
#> -0.0537146 -0.0741390 

## try out bias correction; compare with mod3
(mod3B <- betadisper(dis, groups, type = "median", bias.adjust=TRUE))
#> 
#> 	Homogeneity of multivariate dispersions
#> 
#> Call: betadisper(d = dis, group = groups, type = "median", bias.adjust
#> = TRUE)
#> 
#> No. of Positive Eigenvalues: 15
#> No. of Negative Eigenvalues: 8
#> 
#> Average distance to median:
#>   grazed ungrazed 
#>   0.4055   0.2893 
#> 
#> Eigenvalues for PCoA axes:
#> (Showing 8 of 23 eigenvalues)
#>  PCoA1  PCoA2  PCoA3  PCoA4  PCoA5  PCoA6  PCoA7  PCoA8 
#> 1.7552 1.1334 0.4429 0.3698 0.2454 0.1961 0.1751 0.1284 
anova(mod3B)
#> Analysis of Variance Table
#> 
#> Response: Distances
#>           Df  Sum Sq  Mean Sq F value  Pr(>F)  
#> Groups     1 0.07193 0.071927  3.7826 0.06468 .
#> Residuals 22 0.41834 0.019015                  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
permutest(mod3B, permutations = 99)
#> 
#> Permutation test for homogeneity of multivariate dispersions
#> Permutation: free
#> Number of permutations: 99
#> 
#> Response: Distances
#>           Df  Sum Sq  Mean Sq      F N.Perm Pr(>F)  
#> Groups     1 0.07193 0.071927 3.7826     99   0.05 *
#> Residuals 22 0.41834 0.019015                       
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

## should always work for a single group
group <- factor(rep("grazed", NROW(varespec)))
(tmp <- betadisper(dis, group, type = "median"))
#> 
#> 	Homogeneity of multivariate dispersions
#> 
#> Call: betadisper(d = dis, group = group, type = "median")
#> 
#> No. of Positive Eigenvalues: 15
#> No. of Negative Eigenvalues: 8
#> 
#> Average distance to median:
#> grazed 
#> 0.4255 
#> 
#> Eigenvalues for PCoA axes:
#> (Showing 8 of 23 eigenvalues)
#>  PCoA1  PCoA2  PCoA3  PCoA4  PCoA5  PCoA6  PCoA7  PCoA8 
#> 1.7552 1.1334 0.4429 0.3698 0.2454 0.1961 0.1751 0.1284 
(tmp <- betadisper(dis, group, type = "centroid"))
#> 
#> 	Homogeneity of multivariate dispersions
#> 
#> Call: betadisper(d = dis, group = group, type = "centroid")
#> 
#> No. of Positive Eigenvalues: 15
#> No. of Negative Eigenvalues: 8
#> 
#> Average distance to centroid:
#> grazed 
#> 0.4261 
#> 
#> Eigenvalues for PCoA axes:
#> (Showing 8 of 23 eigenvalues)
#>  PCoA1  PCoA2  PCoA3  PCoA4  PCoA5  PCoA6  PCoA7  PCoA8 
#> 1.7552 1.1334 0.4429 0.3698 0.2454 0.1961 0.1751 0.1284 

## simulate missing values in 'd' and 'group'
## using spatial medians
groups[c(2,20)] <- NA
dis[c(2, 20)] <- NA
mod2 <- betadisper(dis, groups) ## messages
#> missing observations due to 'group' removed
#> missing observations due to 'd' removed
mod2
#> 
#> 	Homogeneity of multivariate dispersions
#> 
#> Call: betadisper(d = dis, group = groups)
#> 
#> No. of Positive Eigenvalues: 14
#> No. of Negative Eigenvalues: 5
#> 
#> Average distance to median:
#>   grazed ungrazed 
#>   0.3984   0.3008 
#> 
#> Eigenvalues for PCoA axes:
#> (Showing 8 of 19 eigenvalues)
#>  PCoA1  PCoA2  PCoA3  PCoA4  PCoA5  PCoA6  PCoA7  PCoA8 
#> 1.4755 0.8245 0.4218 0.3456 0.2159 0.1688 0.1150 0.1060 
permutest(mod2, permutations = 99)
#> 
#> Permutation test for homogeneity of multivariate dispersions
#> Permutation: free
#> Number of permutations: 99
#> 
#> Response: Distances
#>           Df   Sum Sq  Mean Sq      F N.Perm Pr(>F)
#> Groups     1 0.039979 0.039979 2.4237     99   0.16
#> Residuals 18 0.296910 0.016495                     
anova(mod2)
#> Analysis of Variance Table
#> 
#> Response: Distances
#>           Df   Sum Sq  Mean Sq F value Pr(>F)
#> Groups     1 0.039979 0.039979  2.4237 0.1369
#> Residuals 18 0.296910 0.016495               
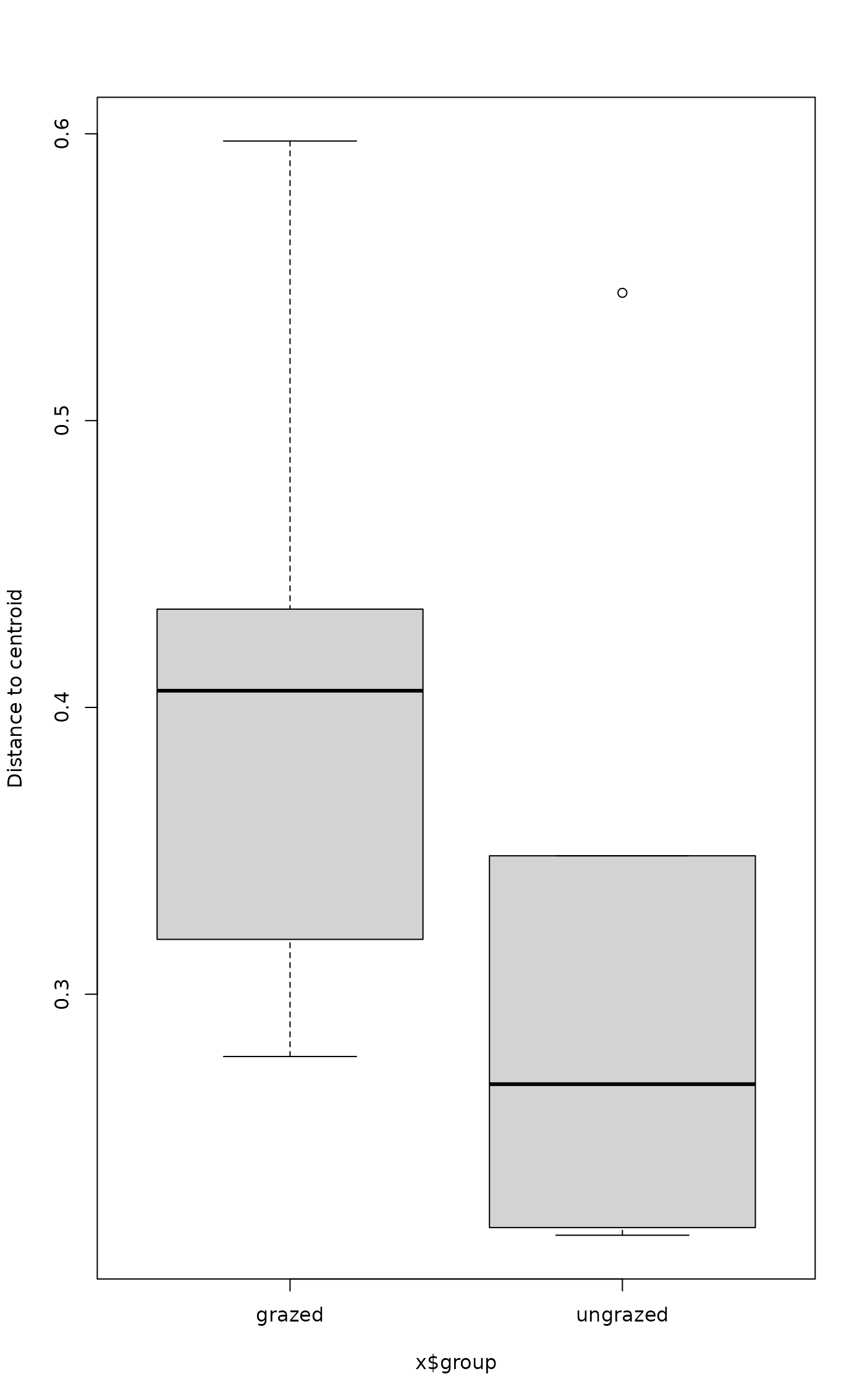
plot(mod2)

boxplot(mod2)

plot(TukeyHSD(mod2))


## Using group centroids
mod3 <- betadisper(dis, groups, type = "centroid")
#> missing observations due to 'group' removed
#> missing observations due to 'd' removed
mod3
#> 
#> 	Homogeneity of multivariate dispersions
#> 
#> Call: betadisper(d = dis, group = groups, type = "centroid")
#> 
#> No. of Positive Eigenvalues: 14
#> No. of Negative Eigenvalues: 5
#> 
#> Average distance to centroid:
#>   grazed ungrazed 
#>   0.4001   0.3108 
#> 
#> Eigenvalues for PCoA axes:
#> (Showing 8 of 19 eigenvalues)
#>  PCoA1  PCoA2  PCoA3  PCoA4  PCoA5  PCoA6  PCoA7  PCoA8 
#> 1.4755 0.8245 0.4218 0.3456 0.2159 0.1688 0.1150 0.1060 
permutest(mod3, permutations = 99)
#> 
#> Permutation test for homogeneity of multivariate dispersions
#> Permutation: free
#> Number of permutations: 99
#> 
#> Response: Distances
#>           Df   Sum Sq  Mean Sq      F N.Perm Pr(>F)
#> Groups     1 0.033468 0.033468 3.1749     99   0.12
#> Residuals 18 0.189749 0.010542                     
anova(mod3)
#> Analysis of Variance Table
#> 
#> Response: Distances
#>           Df   Sum Sq  Mean Sq F value  Pr(>F)  
#> Groups     1 0.033468 0.033468  3.1749 0.09166 .
#> Residuals 18 0.189749 0.010542                  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
plot(mod3)

boxplot(mod3)

plot(TukeyHSD(mod3))