Extrapolated Species Richness in a Species Pool

The functions estimate the extrapolated species richness in a species pool, or the number of unobserved species. Function specpool is based on incidences in sample sites, and gives a single estimate for a collection of sample sites (matrix). Function estimateR is based on abundances (counts) on single sample site.

Usage

specpool(x, pool, smallsample = TRUE)
estimateR(x, ...)
specpool2vect(X, index = c("jack1","jack2", "chao", "boot","Species"))
poolaccum(x, permutations = 100, minsize = 3)
estaccumR(x, permutations = 100, parallel = getOption("mc.cores"))
# S3 method for class 'poolaccum'
summary(object, display, alpha = 0.05, ...)
# S3 method for class 'poolaccum'
plot(x, alpha = 0.05, type = c("l","g"), ...)

Arguments

x: Data frame or matrix with species data or the analysis result for plot function.
pool: A vector giving a classification for pooling the sites in the species data. If missing, all sites are pooled together.
smallsample: Use small sample correction \((N-1)/N\), where \(N\) is the number of sites within the pool.
X, object: A specpool result object.
index: The selected index of extrapolated richness.
permutations: Usually an integer giving the number permutations, but can also be a list of control values for the permutations as returned by the function how, or a permutation matrix where each row gives the permuted indices.
minsize: Smallest number of sampling units reported.
parallel: Number of parallel processes or a predefined socket cluster. With parallel = 1 uses ordinary, non-parallel processing. The parallel processing is done with parallel package.
display: Indices to be displayed.
alpha: Level of quantiles shown. This proportion will be left outside symmetric limits.
type: Type of graph produced in xyplot.
...: Other parameters (not used).

Details

Many species will always remain unseen or undetected in a collection of sample plots. The function uses some popular ways of estimating the number of these unseen species and adding them to the observed species richness (Palmer 1990, Colwell & Coddington 1994).

The incidence-based estimates in specpool use the frequencies of species in a collection of sites. In the following, \(S_P\) is the extrapolated richness in a pool, \(S_0\) is the observed number of species in the collection, \(a_1\) and \(a_2\) are the number of species occurring only in one or only in two sites in the collection, \(p_i\) is the frequency of species \(i\), and \(N\) is the number of sites in the collection. The variants of extrapolated richness in specpool are:

Chao	\(S_P = S_0 + \frac{a_1^2}{2 a_2}\frac{N-1}{N}\)
Chao bias-corrected	\(S_P = S_0 + \frac{a_1(a_1-1)}{2(a_2+1)} \frac{N-1}{N}\)
First order jackknife	\(S_P = S_0 + a_1 \frac{N-1}{N}\)
Second order jackknife	\(S_P = S_0 + a_1 \frac{2N - 3}{N} - a_2 \frac{(N-2)^2}{N (N-1)}\)
Bootstrap	\(S_P = S_0 + \sum_{i=1}^{S_0} (1 - p_i)^N\)

specpool normally uses basic Chao equation, but when there are no doubletons (\(a2=0\)) it switches to bias-corrected version. In that case the Chao equation simplifies to \(S_0 + \frac{1}{2} a_1 (a_1-1) \frac{N-1}{N}\).

The abundance-based estimates in estimateR use counts (numbers of individuals) of species in a single site. If called for a matrix or data frame, the function will give separate estimates for each site. The two variants of extrapolated richness in estimateR are bias-corrected Chao and ACE (O'Hara 2005, Chiu et al. 2014). The Chao estimate is similar as the bias corrected one above, but \(a_i\) refers to the number of species with abundance \(i\) instead of number of sites, and the small-sample correction is not used. The ACE estimate is defined as:

ACE	\(S_P = S_{abund} + \frac{S_{rare}}{C_{ace}}+ \frac{a_1}{C_{ace}} \gamma^2_{ace}\)
where	\(C_{ace} = 1 - \frac{a_1}{N_{rare}}\)
	\(\gamma^2_{ace} = \max \left[ \frac{S_{rare} \sum_{i=1}^{10} i(i-1)a_i}{C_{ace} N_{rare} (N_{rare} - 1)}-1, 0 \right]\)

Here \(a_i\) refers to number of species with abundance \(i\) and \(S_{rare}\) is the number of rare species, \(S_{abund}\) is the number of abundant species, with an arbitrary threshold of abundance 10 for rare species, and \(N_{rare}\) is the number of individuals in rare species.

Functions estimate the standard errors of the estimates. These only concern the number of added species, and assume that there is no variance in the observed richness. The equations of standard errors are too complicated to be reproduced in this help page, but they can be studied in the R source code of the function and are discussed in the vignette that can be read with the browseVignettes("vegan"). The standard error are based on the following sources: Chiu et al. (2014) for the Chao estimates and Smith and van Belle (1984) for the first-order Jackknife and the bootstrap (second-order jackknife is still missing). For the variance estimator of \(S_{ace}\) see O'Hara (2005).

Functions poolaccum and estaccumR are similar to specaccum, but estimate extrapolated richness indices of specpool or estimateR in addition to number of species for random ordering of sampling units. Function specpool uses presence data and estaccumR count data. The functions share summary and plot methods. The summary returns quantile envelopes of permutations corresponding the given level of alpha and standard deviation of permutations for each sample size. NB., these are not based on standard deviations estimated within specpool or estimateR, but they are based on permutations. The plot function shows the mean and envelope of permutations with given alpha for models. The selection of models can be restricted and order changes using the display argument in summary or plot. For configuration of plot command, see xyplot.

Value

Function specpool returns a data frame with entries for observed richness and each of the indices for each class in pool vector. The utility function specpool2vect maps the pooled values into a vector giving the value of selected index for each original site. Function estimateR returns the estimates and their standard errors for each site. Functions poolaccum and estimateR return matrices of permutation results for each richness estimator, the vector of sample sizes and a table of means of permutations for each estimator.

References

Chao, A. (1987). Estimating the population size for capture-recapture data with unequal catchability. Biometrics 43, 783–791.

Chiu, C.H., Wang, Y.T., Walther, B.A. & Chao, A. (2014). Improved nonparametric lower bound of species richness via a modified Good-Turing frequency formula. Biometrics 70, 671–682.

Colwell, R.K. & Coddington, J.A. (1994). Estimating terrestrial biodiversity through extrapolation. Phil. Trans. Roy. Soc. London B 345, 101–118.

O'Hara, R.B. (2005). Species richness estimators: how many species can dance on the head of a pin? J. Anim. Ecol. 74, 375–386.

Palmer, M.W. (1990). The estimation of species richness by extrapolation. Ecology 71, 1195–1198.

Smith, E.P & van Belle, G. (1984). Nonparametric estimation of species richness. Biometrics 40, 119–129.

Author

Bob O'Hara (estimateR) and Jari Oksanen.

Note

The functions are based on assumption that there is a species pool: The community is closed so that there is a fixed pool size \(S_P\). In general, the functions give only the lower limit of species richness: the real richness is \(S >= S_P\), and there is a consistent bias in the estimates. Even the bias-correction in Chao only reduces the bias, but does not remove it completely (Chiu et al. 2014).

Optional small sample correction was added to specpool in vegan 2.2-0. It was not used in the older literature (Chao 1987), but it is recommended recently (Chiu et al. 2014).

Examples

data(dune)
data(dune.env)
pool <- with(dune.env, specpool(dune, Management))
pool
#>    Species     chao   chao.se    jack1 jack1.se    jack2     boot  boot.se n
#> BF      16 17.19048 1.5895675 19.33333 2.211083 19.83333 17.74074 1.646379 3
#> HF      21 21.51429 0.9511693 23.40000 1.876166 22.05000 22.56864 1.821518 5
#> NM      21 22.87500 2.1582871 26.00000 3.291403 25.73333 23.77696 2.300982 6
#> SF      21 29.88889 8.6447967 27.66667 3.496029 31.40000 23.99496 1.850288 6
op <- par(mfrow=c(1,2))
boxplot(specnumber(dune) ~ Management, data = dune.env,
        col = "hotpink", border = "cyan3")
boxplot(specnumber(dune)/specpool2vect(pool) ~ Management,
        data = dune.env, col = "hotpink", border = "cyan3")

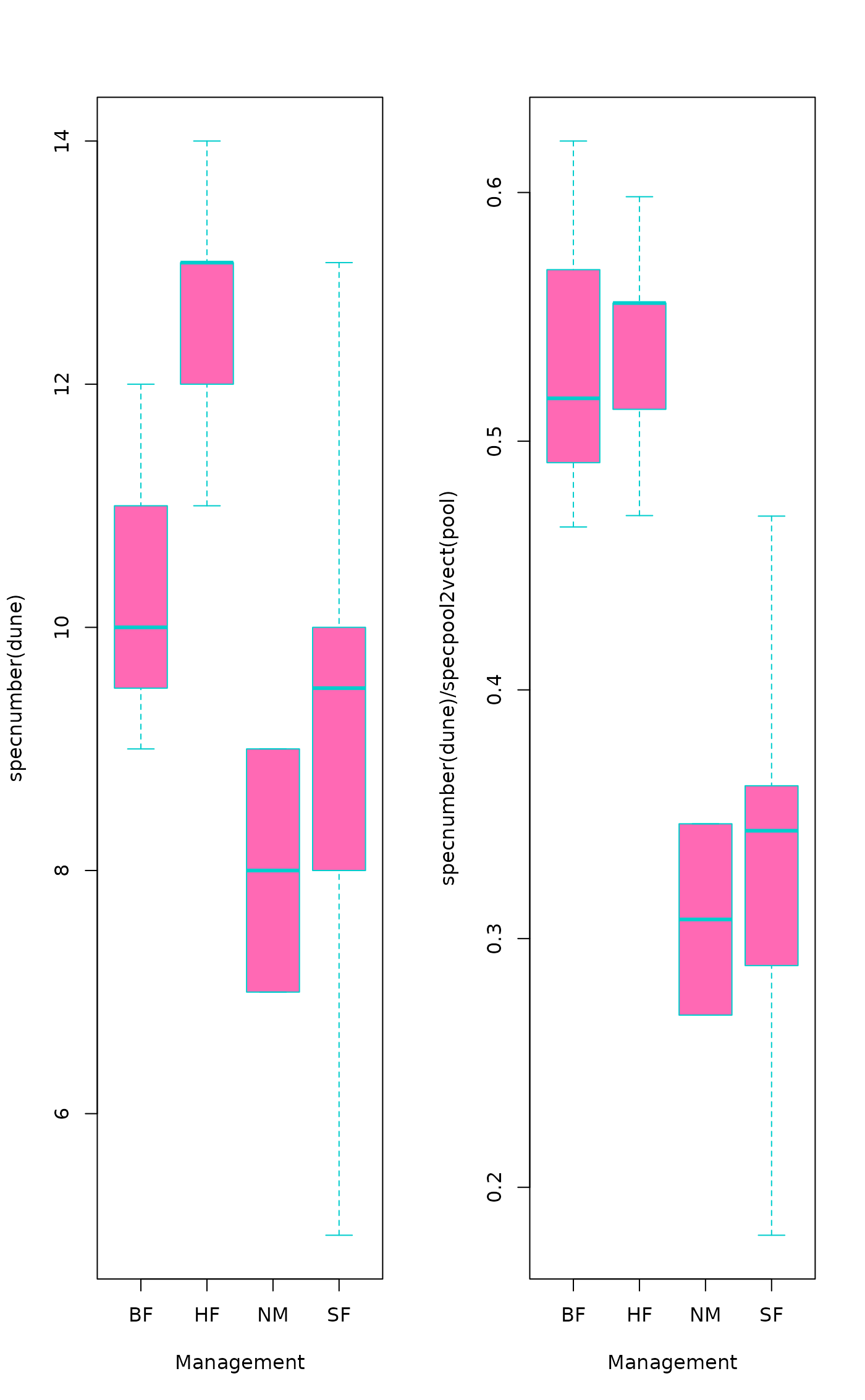par(op)
data(BCI)
## Accumulation model
pool <- poolaccum(BCI)
summary(pool, display = "chao")
#> $chao
#>        N     Chao     2.5%    97.5%   Std.Dev
#>  [1,]  3 162.2553 144.4502 182.0259 11.503284
#>  [2,]  4 175.8180 156.4219 197.9883 10.981622
#>  [3,]  5 183.2546 164.2696 210.0542 12.137610
#>  [4,]  6 189.1523 170.8417 213.5829 11.503909
#>  [5,]  7 195.3049 176.4527 226.6597 13.074074
#>  [6,]  8 197.6205 179.4098 221.7531 11.187533
#>  [7,]  9 201.0709 180.4597 224.2972 11.165732
#>  [8,] 10 205.5505 188.7866 227.1853 11.192582
#>  [9,] 11 208.4693 190.3031 230.5120 12.330274
#> [10,] 12 210.9969 190.5683 232.1458 11.641705
#> [11,] 13 214.3047 194.2058 241.6639 12.224990
#> [12,] 14 216.1883 195.0731 240.2505 12.307217
#> [13,] 15 219.0240 197.8400 245.8404 11.907296
#> [14,] 16 221.6877 201.3524 249.8191 13.494091
#> [15,] 17 222.8829 202.4674 248.9174 15.155467
#> [16,] 18 224.0407 205.1279 257.4424 13.218161
#> [17,] 19 225.6845 207.3639 254.6342 13.178512
#> [18,] 20 228.1225 208.9622 259.0367 13.332857
#> [19,] 21 228.6610 209.8250 254.3313 12.833261
#> [20,] 22 229.2710 210.3460 249.0345 11.246646
#> [21,] 23 230.3813 211.2286 257.8359 11.255424
#> [22,] 24 231.1036 209.5530 254.8051 10.670897
#> [23,] 25 232.8775 211.5198 255.8912 11.270560
#> [24,] 26 234.1728 213.7274 260.9693 12.050982
#> [25,] 27 235.0748 215.6529 264.5753 12.147563
#> [26,] 28 236.6850 218.6506 268.0165 12.220517
#> [27,] 29 237.4003 216.9410 270.4329 12.993964
#> [28,] 30 236.5526 219.3734 265.7913 11.784562
#> [29,] 31 236.4392 219.1514 260.2008 10.543600
#> [30,] 32 237.2727 221.2701 263.1505 13.029316
#> [31,] 33 237.1201 221.4075 260.2984 11.011873
#> [32,] 34 236.9519 222.0721 258.7285 11.324032
#> [33,] 35 237.5450 222.9849 261.4903 10.547915
#> [34,] 36 237.5977 223.3364 258.7115  8.862824
#> [35,] 37 238.1719 223.5616 261.6496  9.624955
#> [36,] 38 238.2845 223.3463 258.6590  9.360541
#> [37,] 39 237.9446 224.4921 255.3324  8.526508
#> [38,] 40 237.8012 224.7824 253.9266  7.521096
#> [39,] 41 237.6671 225.9334 252.1478  6.888923
#> [40,] 42 237.0876 225.1039 249.4445  6.357136
#> [41,] 43 237.2275 225.6064 247.6340  5.904975
#> [42,] 44 237.1937 226.7373 247.3899  5.435124
#> [43,] 45 237.2685 226.7906 247.9472  5.431733
#> [44,] 46 237.1068 228.6081 247.0945  4.779439
#> [45,] 47 237.3225 229.4321 245.5399  3.972105
#> [46,] 48 237.2380 229.2102 244.9243  3.552839
#> [47,] 49 237.0709 233.7959 245.4082  3.099847
#> [48,] 50 236.3732 236.3732 236.3732  0.000000
#> 
#> attr(,"class")
#> [1] "summary.poolaccum"
plot(pool)

## Quantitative model
estimateR(BCI[1:5,])
#>                   1          2          3          4          5
#> S.obs     93.000000  84.000000  90.000000  94.000000 101.000000
#> S.chao1  117.473684 117.214286 141.230769 111.550000 136.000000
#> se.chao1  11.583785  15.918953  23.001405   8.919663  15.467344
#> S.ACE    122.848959 117.317307 134.669844 118.729941 137.114088
#> se.ACE     5.736054   5.571998   6.191618   5.367571   5.848474