Analysis of Similarities

Analysis of similarities (ANOSIM) provides a way to test statistically whether there is a significant difference between two or more groups of sampling units.

Usage

anosim(x, grouping, permutations = 999, distance = "bray", strata = NULL,
    parallel = getOption("mc.cores"))

Arguments

x: Data matrix or data frame in which rows are samples and columns are response variable(s), or a dissimilarity object or a symmetric square matrix of dissimilarities.
grouping: Factor for grouping observations.
permutations: a list of control values for the permutations as returned by the function how, or the number of permutations required, or a permutation matrix where each row gives the permuted indices.
distance: Choice of distance metric that measures the dissimilarity between two observations. See vegdist for options. This will be used if x was not a dissimilarity structure or a symmetric square matrix.
strata: An integer vector or factor specifying the strata for permutation. If supplied, observations are permuted only within the specified strata.
parallel: Number of parallel processes or a predefined socket cluster. With parallel = 1 uses ordinary, non-parallel processing. The parallel processing is done with parallel package.

Details

Analysis of similarities (ANOSIM) provides a way to test statistically whether there is a significant difference between two or more groups of sampling units. Function anosim operates directly on a dissimilarity matrix. A suitable dissimilarity matrix is produced by functions dist or vegdist. The method is philosophically allied with NMDS ordination (monoMDS), in that it uses only the rank order of dissimilarity values.

If two groups of sampling units are really different in their species composition, then compositional dissimilarities between the groups ought to be greater than those within the groups. The anosim statistic $R$ is based on the difference of mean ranks between groups ($r_B$) and within groups ($r_W$):

$$R = (r_B - r_W)/(N (N-1) / 4)$$

The divisor is chosen so that $R$ will be in the interval $-1 \dots +1$, value $0$ indicating completely random grouping.

The statistical significance of observed $R$ is assessed by permuting the grouping vector to obtain the empirical distribution of $R$ under null-model. See permutations for additional details on permutation tests in Vegan. The distribution of simulated values can be inspected with the permustats function.

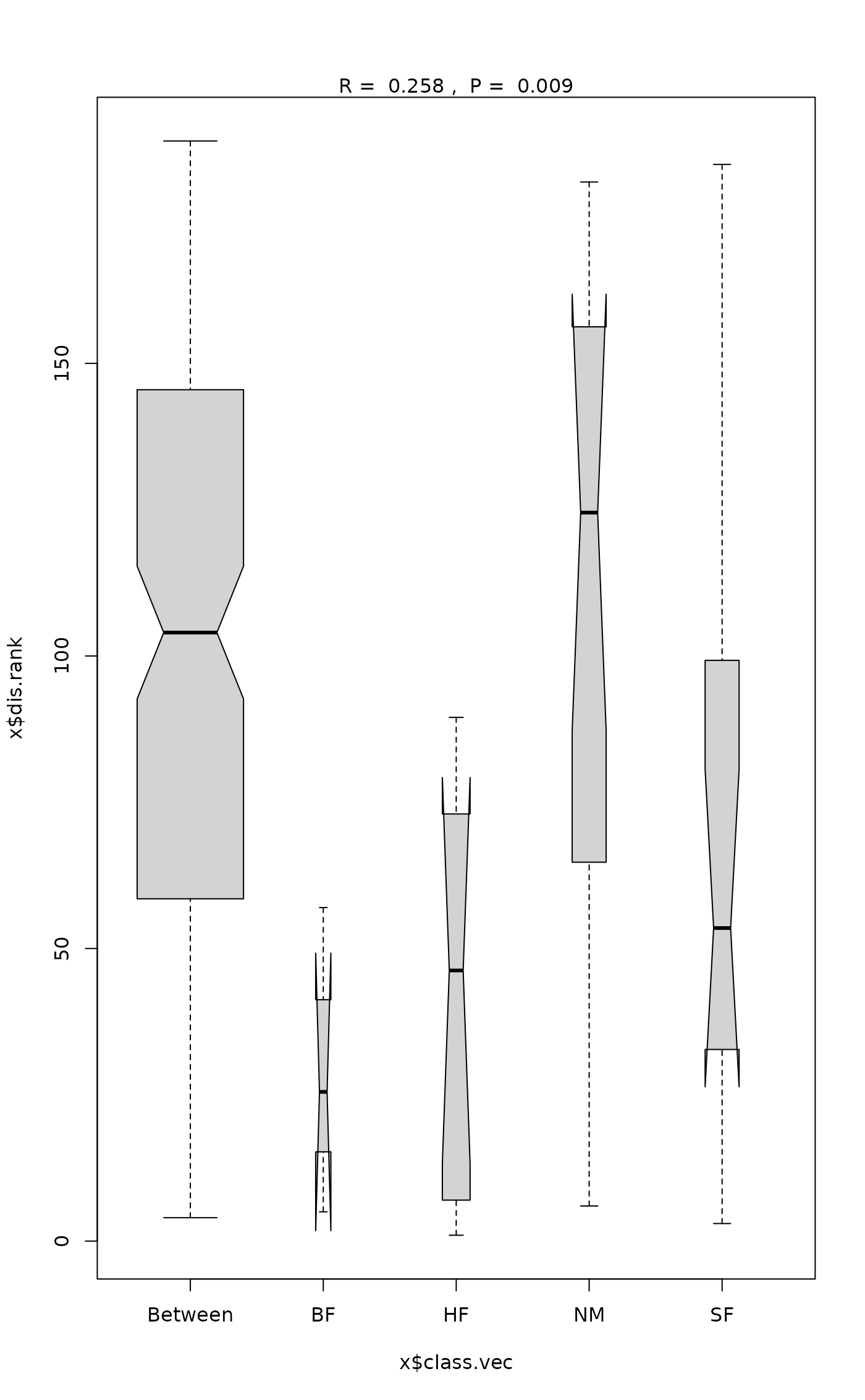
The function has summary and plot methods. These both show valuable information to assess the validity of the method: The function assumes that all ranked dissimilarities within groups have about equal median and range. The plot method uses boxplot with options notch=TRUE and varwidth=TRUE.

Value

The function returns a list of class "anosim" with following items:

call: Function call.
statistic: The value of ANOSIM statistic $R$
signif: Significance from permutation.
perm: Permutation values of $R$. The distribution of permutation values can be inspected with function permustats.
class.vec: Factor with value Between for dissimilarities between classes and class name for corresponding dissimilarity within class.
dis.rank: Rank of dissimilarity entry.
dissimilarity: The name of the dissimilarity index: the "method" entry of the dist object.
control: A list of control values for the permutations as returned by the function how.

References

Clarke, K. R. (1993). Non-parametric multivariate analysis of changes in community structure. Australian Journal of Ecology 18, 117–143.

Warton, D.I., Wright, T.W., Wang, Y. 2012. Distance-based multivariate analyses confound location and dispersion effects. Methods in Ecology and Evolution, 3, 89–101

Author

Jari Oksanen, with a help from Peter R. Minchin.

Note

The anosim function can confound the differences between groups and dispersion within groups and the results can be difficult to interpret (cf. Warton et al. 2012). The function returns a lot of information to ease studying its performance. Most anosim models could be analysed with adonis2 which seems to be a more robust alternative.

Examples

data(dune)
data(dune.env)
dune.dist <- vegdist(dune)
dune.ano <- with(dune.env, anosim(dune.dist, Management))
summary(dune.ano)
#> 
#> Call:
#> anosim(x = dune.dist, grouping = Management) 
#> Dissimilarity: bray 
#> 
#> ANOSIM statistic R: 0.2579 
#>       Significance: 0.009 
#> 
#> Permutation: free
#> Number of permutations: 999
#> 
#> Upper quantiles of permutations (null model):
#>   90%   95% 97.5%   99% 
#> 0.121 0.164 0.205 0.242 
#> 
#> Dissimilarity ranks between and within classes:
#>         0%   25%    50%     75%  100%   N
#> Between  4 58.50 104.00 145.500 188.0 147
#> BF       5 15.25  25.50  41.250  57.0   3
#> HF       1  7.25  46.25  68.125  89.5  10
#> NM       6 64.75 124.50 156.250 181.0  15
#> SF       3 32.75  53.50  99.250 184.0  15
#> 
plot(dune.ano)
#> Warning: some notches went outside hinges ('box'): maybe set notch=FALSE