Mitchell-Olds and Shaw Test for the Location of Quadratic Extreme

Mitchell-Olds & Shaw test concerns the location of the highest (hump) or lowest (pit) value of a quadratic curve at given points. Typically, it is used to study whether the quadratic hump or pit is located within a studied interval. The current test is generalized so that it applies generalized linear models (glm) with link function instead of simple quadratic curve. The test was popularized in ecology for the analysis of humped species richness patterns (Mittelbach et al. 2001), but it is more general. With logarithmic link function, the quadratic response defines the Gaussian response model of ecological gradients (ter Braak & Looman 1986), and the test can be used for inspecting the location of Gaussian optimum within a given range of the gradient. It can also be used to replace Tokeshi's test of “bimodal” species frequency distribution.

Usage

MOStest(x, y, interval, ...)
# S3 method for class 'MOStest'
plot(x, which = c(1,2,3,6), ...)
fieller.MOStest(object, level = 0.95)
# S3 method for class 'MOStest'
profile(fitted, alpha = 0.01, maxsteps = 10, del = zmax/5, ...)
# S3 method for class 'MOStest'
confint(object, parm = 1, level = 0.95, ...)

Arguments

x: The independent variable or plotting object in plot.
y: The dependent variable.
interval: The two points at which the test statistic is evaluated. If missing, the extremes of x are used.
which: Subset of plots produced. Values which=1 and 2 define plots specific to MOStest (see Details), and larger values select graphs of plot.lm (minus 2).
object, fitted: A result object from MOStest.
level: The confidence level required.
alpha: Maximum significance level allowed.
maxsteps: Maximum number of steps in the profile.
del: A step length parameter for the profile (see code).
parm: Ignored.
...: Other variables passed to functions. Function MOStest passes these to glm so that these can include family. The other functions pass these to underlying graphical functions.

Details

The function fits a quadratic curve \(\mu = b_0 + b_1 x + b_2 x^2\) with given family and link function. If \(b_2 < 0\), this defines a unimodal curve with highest point at \(u = -b_1/(2 b_2)\) (ter Braak & Looman 1986). If \(b_2 > 0\), the parabola has a minimum at \(u\) and the response is sometimes called “bimodal”. The null hypothesis is that the extreme point \(u\) is located within the interval given by points \(p_1\) and \(p_2\). If the extreme point \(u\) is exactly at \(p_1\), then \(b_1 = 0\) on shifted axis \(x - p_1\). In the test, origin of x is shifted to the values \(p_1\) and \(p_2\), and the test statistic is based on the differences of deviances between the original model and model where the origin is forced to the given location using the standard anova.glm function (Oksanen et al. 2001). Mitchell-Olds & Shaw (1987) used the first degree coefficient with its significance as estimated by the summary.glm function. This give identical results with Normal error, but for other error distributions it is preferable to use the test based on differences in deviances in fitted models.

The test is often presented as a general test for the location of the hump, but it really is dependent on the quadratic fitted curve. If the hump is of different form than quadratic, the test may be insignificant.

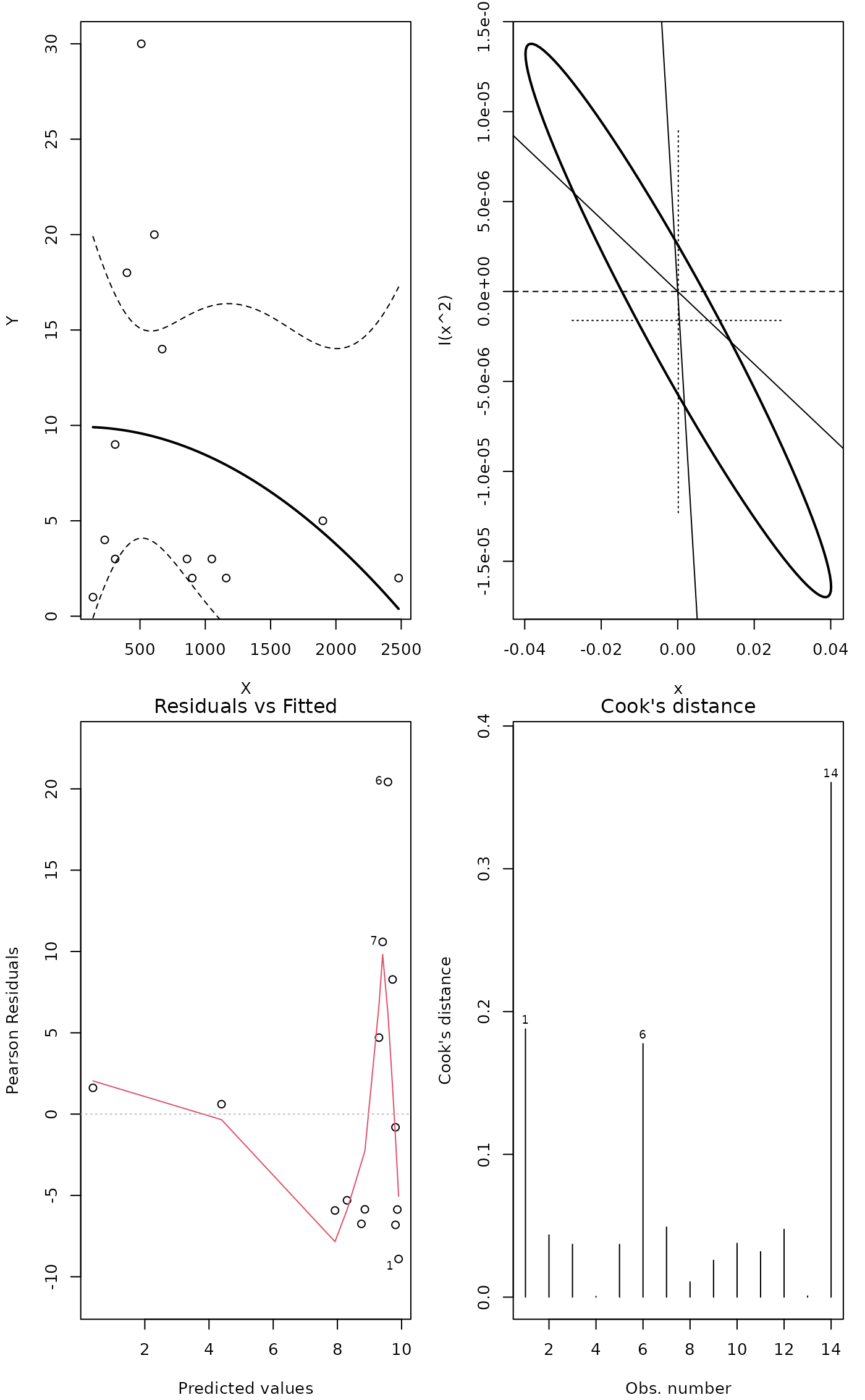
Because of strong assumptions in the test, you should use the support functions to inspect the fit. Function plot(..., which=1) displays the data points, fitted quadratic model, and its approximate 95% confidence intervals (2 times SE). Function plot with which = 2 displays the approximate confidence interval of the polynomial coefficients, together with two lines indicating the combinations of the coefficients that produce the evaluated points of x. Moreover, the cross-hair shows the approximate confidence intervals for the polynomial coefficients ignoring their correlations. Higher values of which produce corresponding graphs from plot.lm. That is, you must add 2 to the value of which in plot.lm.

Function fieller.MOStest approximates the confidence limits of the location of the extreme point (hump or pit) using Fieller's theorem following ter Braak & Looman (1986). The test is based on quasideviance except if the family is poisson or binomial. Function profile evaluates the profile deviance of the fitted model, and confint finds the profile based confidence limits following Oksanen et al. (2001).

The test is typically used in assessing the significance of diversity hump against productivity gradient (Mittelbach et al. 2001). It also can be used for the location of the pit (deepest points) instead of the Tokeshi test. Further, it can be used to test the location of the the Gaussian optimum in ecological gradient analysis (ter Braak & Looman 1986, Oksanen et al. 2001).

Value

The function is based on glm, and it returns the result of object of glm amended with the result of the test. The new items in the MOStest are:

isHump: TRUE if the response is a hump.
isBracketed: TRUE if the hump or the pit is bracketed by the evaluated points.
hump: Sorted vector of location of the hump or the pit and the points where the test was evaluated.
coefficients: Table of test statistics and their significances.

References

Mitchell-Olds, T. & Shaw, R.G. 1987. Regression analysis of natural selection: statistical inference and biological interpretation. Evolution 41, 1149–1161.

Mittelbach, G.C. Steiner, C.F., Scheiner, S.M., Gross, K.L., Reynolds, H.L., Waide, R.B., Willig, R.M., Dodson, S.I. & Gough, L. 2001. What is the observed relationship between species richness and productivity? Ecology 82, 2381–2396.

Oksanen, J., Läärä, E., Tolonen, K. & Warner, B.G. 2001. Confidence intervals for the optimum in the Gaussian response function. Ecology 82, 1191–1197.

ter Braak, C.J.F & Looman, C.W.N 1986. Weighted averaging, logistic regression and the Gaussian response model. Vegetatio 65, 3–11.

Author

Jari Oksanen

Note

Function fieller.MOStest is based on package optgrad in the Ecological Archives (https://figshare.com/articles/dataset/Full_Archive/3521975) accompanying Oksanen et al. (2001). The Ecological Archive package optgrad also contains profile deviance method for the location of the hump or pit, but the current implementation of profile and confint rather follow the example of profile.glm and confint.glm in the MASS package.

Examples

## The Al-Mufti data analysed in humpfit():
mass <- c(140,230,310,310,400,510,610,670,860,900,1050,1160,1900,2480)
spno <- c(1,  4,  3,  9, 18, 30, 20, 14,  3,  2,  3,  2,  5,  2)
mod <- MOStest(mass, spno)
## Insignificant
mod
#> 
#> Mitchell-Olds and Shaw test
#> Null: hump of a quadratic linear predictor is at min or max
#> 
#> Family: gaussian 
#> Link function: identity 
#> 
#>       hump        min        max 
#>   46.89749  140.00000 2480.00000 
#> ***** Caution: hump/pit not bracketed by the data ******
#> 
#>             min/max      F Pr(>F)
#> hump at min     140 0.0006 0.9816
#> hump at max    2480 0.3161 0.5852
#> Combined                   0.9924
## ... but inadequate shape of the curve
op <- par(mfrow=c(2,2), mar=c(4,4,1,1)+.1)
plot(mod)

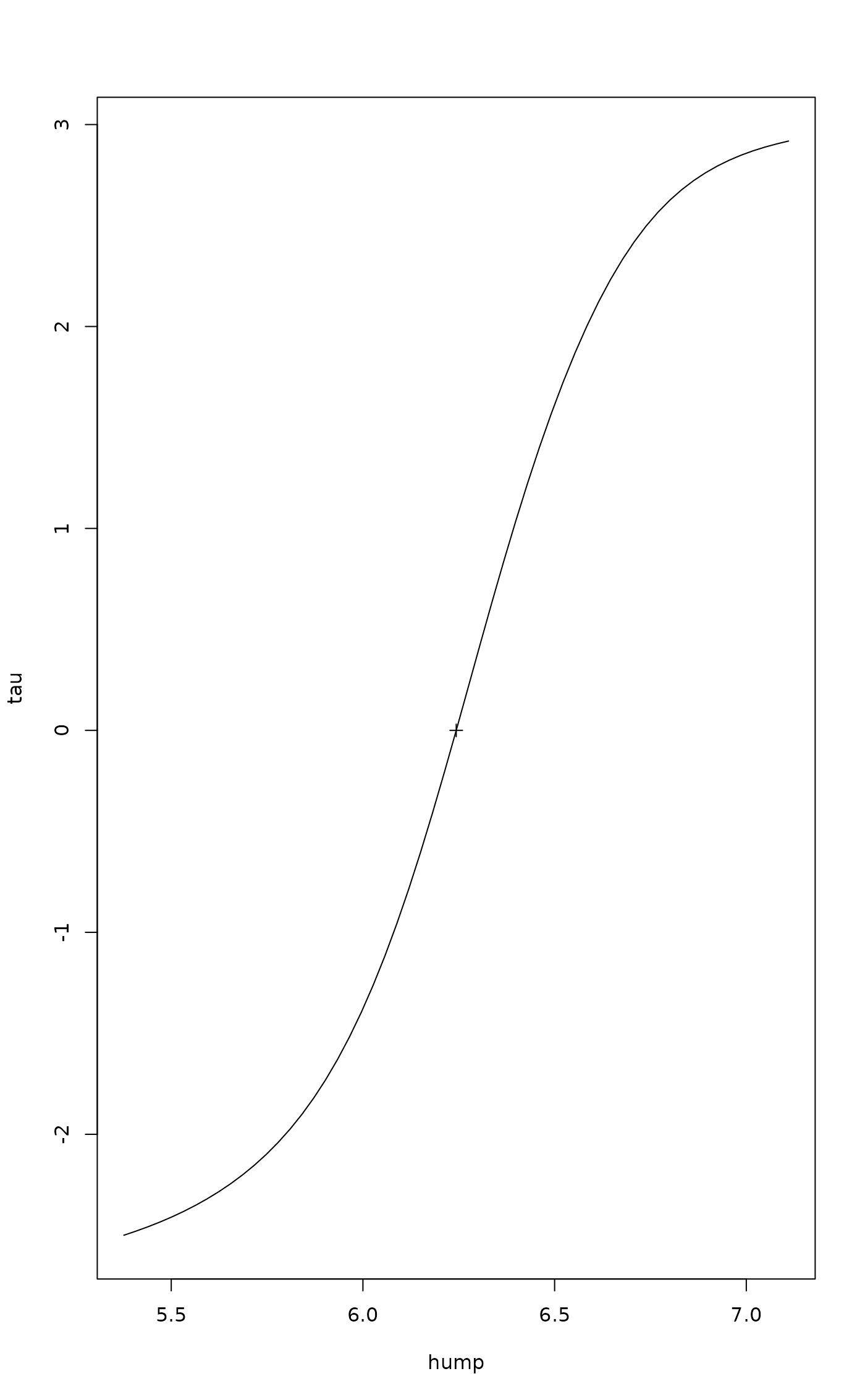
## Looks rather like log-link with Poisson error and logarithmic biomass
mod <- MOStest(log(mass), spno, family=quasipoisson)
mod
#> 
#> Mitchell-Olds and Shaw test
#> Null: hump of a quadratic linear predictor is at min or max
#> 
#> Family: quasipoisson 
#> Link function: log 
#> 
#>      min     hump      max 
#> 4.941642 6.243371 7.816014 
#> 
#>             min/max      F  Pr(>F)  
#> hump at min  4.9416 7.1367 0.02174 *
#> hump at max  7.8160 9.0487 0.01191 *
#> Combined                   0.03338 *
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
plot(mod)

par(op)
## Confidence Limits
fieller.MOStest(mod)
#>    2.5 %   97.5 % 
#> 5.255827 6.782979 
confint(mod)
#>    2.5 %   97.5 % 
#> 5.816021 6.574378 
plot(profile(mod))